Subject: 3D Star calculation
Hi,
I am looking for a formula that will give me a layout for a 3 dimensional 5 pointed star. I want to form it out of sheet metal, using 5 polygons and soldering them at the apex. Can you please help me with this? I would like to be able to give the formula the height of the star from the bottom two points to the top point and also how deep the star is. Thank you very much!
Sincerely,
Kent Lightcrafters, Inc.
Hi Kent
I made a cardboard model of the star. Instructions for making a cardboard star.
Kent completed his star and sent us a picture that we put in the Resource Room.

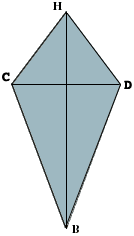
Placing the star on a sheet of paper and tracing around its edges you get the diagram below.
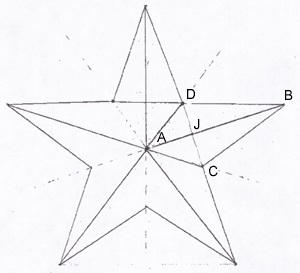
The center of the star is directly above A, a distance of h, at a point we'll call H. We have two more variables:
c: the distance from A to C.
Now we want to determine the dimensions of the sheet of metal to cut out:
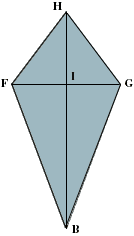 |
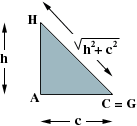
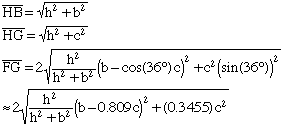 The lines HB and FG are perpendicular. The calculations are given below. |
The two diagrams below are side views. Notice that the angle HIJ is a right angle.
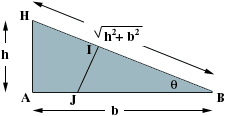 |
 |
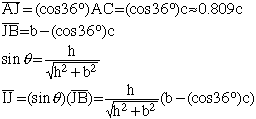
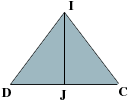
The diagram below is an end view.
 |
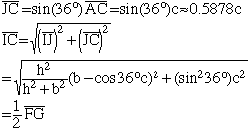 |
If we know the ratios of h, b, and c we can simplify the formulas. In my drawings h = c = 0.4b so b = 2.5h.
Substituting into the formulas I get
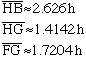
Judi
In August of 2019 we received the following from Mike.
I have been looking at the 3D star layout math by Judi.
Plugging in my numbers in her formulae, I can't get anywhere close to what I think the dimensions should be. Is there an updated tutorial for laying out a 3D star?
Thank You,
Mike
Hi Mike,
I haven't looked at Judi's formulae in a number of years. Can you send me the numbers you are using and I will tri to see if I can diagnose the problem.
Harley
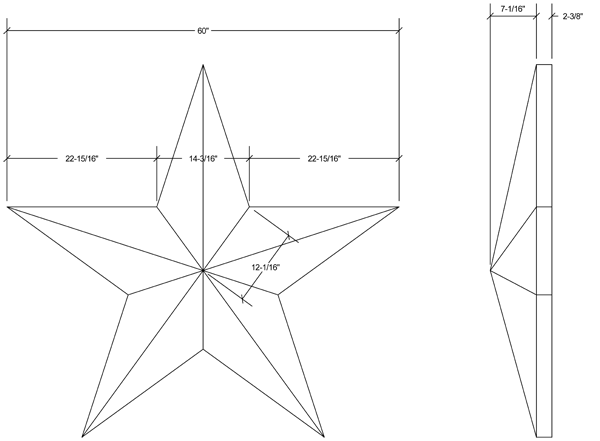
Here is a drawing of the star, they are for street light poles.
Hope this works!
Thanks again.Mike
Hi Mike,
The situation you have is much different from what Judi had in her question from Kent. In your situation I would suggest a different approach.
I am going to use the lettering in Judi's diagram below with your dimensions. Hence $|AD| = 12 \large \frac{1}{16}$ inches and $H$ is the center of the star is $7 \large \frac{1}{16}$ inches above $A.$

Looking from the side the triangle $ADH$ is a right triangle so I can use Pythagoras Theorem to determine $|AD|.$
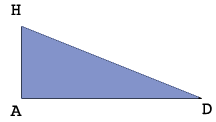
$|AH| = 7.0625 \mbox{ and } |AD| = 12.0625,$ both in inches so
\[|DH|^2 = 7.0625^2 + 12.0625^2 \mbox{ and hence } |DH| = 13.9779 \mbox{ inches.}\]
Triangle $BHA$ is also a right triangle so I can use Pythagoras Theorem to determine $|BH|$ if I can first find $|BA|.$
The measure of the angle $DAB$ is $36^o$ and hence the Law of Cosines for triangle $BDA$ gives
\[|BD|^2 = |DA|^2 + |AB|^2 - 2 \times |DA| \times |AB| \times \cos(36^o).\]
Letting $d = |AB|,$ and substituting the values you have and simplifying I get the quadratic equation
\[d^2 - 19,5175 d - 380.625 = 0.\]
Solving with the general quadratic I get $d = 31.5729$ inches. (The negative solution is impossible.)
Finally Pythagoras Theorem on triangle $BHA$ gives
\[|BH| = \sqrt{7,0625^2 + 31.5729^2} = 32.3532 \mbox{ inches.}\]
Hence the layout for each of the five pieces to form the star is below.
Rounding the dimensions to sixteenth of an inch the dimensions are $|BH| = 32 \large \frac{3}{8}$ inches, $|BD| = 22 \large \frac{15}{16}$ inches, and $|DH| = 14$ inches.
I hope this helps,
Harley