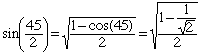Name: Kent
Who is asking: Parent
Level: Secondary
Question: My daughter has a Circle problem: A circle of 30 in. diameter has an octagon (8 equal chords) inscribed in it. What is the length of each chord?
My method of solving this problemis rather difficult for her to follow. Can you help?
Hi Kent,
The best approach depends on how much trigonometry one knows. In a circle
of radius r, the length of the chord that subtends a central angle x is
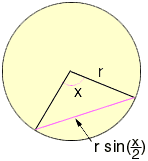
The regular octagon has a central angle of 360/8 = 45 degrees. Since your circle has radius 30, its side has length chord = 30 sin(22.5), which equals approximately 11.48.
An approach that uses more geometry is to know that
sin 45 = cos 45 = 
and the identity that
Then
