Student question, Grade 12 level
A polynomial function is described by the following conditions: f(x) has two real zeros at x= -2 and x= 1, each of multiplicity 2 f(x) has two complex zeros as x goes to -infinity, f(x) goes to +infinity as x goes to +infinity, f(x) goes to +infinity f(x) has a y-intercept at (0,2)
Sketch a polynomial function that satisfies the above conditions.
Write an equation for function f(x)
Write another function g(x) that also satisfies the above parameters.
Thanks!
Hi
Where I am today I don't have a very good drawing tool so my graphs aren't very smooth.
Your polynomial has at least 6 zeros, a double zero of multiplicity 2 at -2, a zero of multiplicity 2 at 1 and 2 complex zeros. Thus the polynomial must have degree at least 6. "As x goes to -infinity, f(x) goes to +infinity" implies that as x gets large and negative, y gets large and positive, so for large negative values of x the graph is in the second quadrant. This allows me to draw a rough sketch of what the graph might look like. Starting in the second quadrant draw a graph with enough peaks and valleys that it crosses the x-axis 6 times (6 times because it has 6 roots)
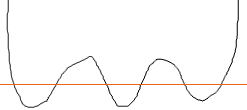
This sketch has the property that "as x goes to -infinity, f(x) goes to +infinity" and "as x goes to +infinity, f(x) goes to +infinity" but the zero are not correct. A zero of multiplicity 2 results when a peak or valley just touches the x-axis as in the diagrams below.
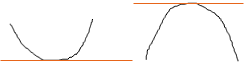
and complex zeros result when a peak or valley does not extend far enough for the curve to cross the x-axis. Hence the graph might look like
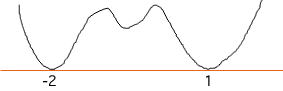
To finish the sketch you need to put the y-axis somewhere so that the graph passes through (0,2).
For the algebra part of the problem you know that f(x) is a polynomial of degree 6. You also know that it has "a double zero of multiplicity 2 at -2" and "a zero of multiplicity 2 at 1". Hence you can factor f(x) and get the 4 factors
Can you find a, b and c so that all the conditions are satisfied?
Peny