Maria
student (10-12)

This question was given to us as a bonus. No one in our class got it right, would you please send an answer and explain how you arrived at the answer. Thank you.

A health club with a membership of 650 people operates a running track and an indoor swimming pool. A survey of the membership indicates that 68% use the running track, 44% use the swimming pool, and 8% use neither. If a member is chosen at random, what is the prbability that the member uses:

a) Both the track and the pool?

b) Only the track?

I would start by drawing a diagram to represent the memberships. The diagram I am going to draw is called a Venn Diagram.

Draw a rectangle to contain the 650 members. Inside the rectangle draw two circles. Inside the circle labeled T are the members who use the track and inside the circle labeled P are the members who use the pool.

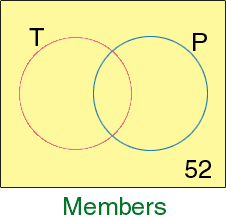
8% of 650 is 52, so 52 members are not in either circle. Record the 52 on the diagram. Thus there are 650 - 52 = 598 members who either use the track or the pool.

68% of 650 is 442, hence there are 442 members inside the "T" circle.
44% of 650 is 286, hence there are 286 members inside the "P" circle.

The difficulty here is that 442 + 286 = 728 and we know that there are only 598 in the two circles. This apparent discrepancy arises since the members who are inside both circles have been counted twice. Once because they use the track and once becaude they use the pool.

You need to put numbers into the three remaining regions of the diagram, the region inside T but outside P, the region inside P but outside T and the region which is in both T and P. I have called these numbers a, b and c in the diagram below.

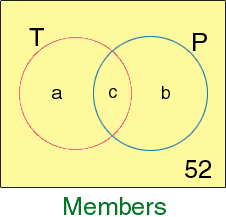
You know that

Once you know a, b and c you can find the probabilities.