Name: Monty

Who is asking: Other
Level: Middle

Question: This problem is from a ninth grade Math book:

"Essentials of Mathematics" Russell V. Person. c. 1961 Second Pr. 1963

My neighbors daughter asked for my help with this homework problem in 1964.

===============================

35. A man and his wife walk up a moving escalator. The man walks twice as fast as his wife. When he arrives at the top, he has taken 28 steps. When she arrives at the top, she has taken 21 steps. How many steps are visible in the escalator at any one time.

==============================

This is just for fun, it's not critical.

Also, do they have problems this hard in ninth grade nowadays?

Monty

PS I doubt that you will need it but I'll send the solution if you do.

This is a great problem. Here is our solution.

Just as they step on the escalator paint the first step red so that you can see how it progresses relative to how they progress. We then drew a diagram of the situation just as the man reaches the top.

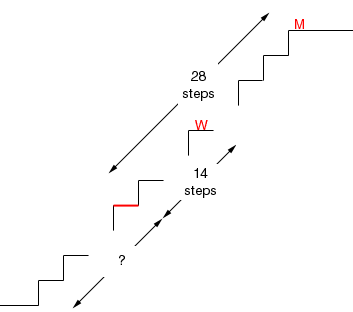
The man has walked up 28 steps so the red step is 28 steps behind him. The woman walks at half his speed so she is 14 steps above the red step. Thus the woman is still 14 steps from the top.

Now look at the diagram again. In the time it took the red step to raise the distance labeled ?, the woman has climbed 14 steps. Since the escalator and the woman are travelling at the same rate, ? is 14. Hence you can see 28 + 14 = 42 steps.

Is this how you solved the problem?

We are not sure about the difficulty of grade nine problems, but we do teach a course to students who plan to be elementary school teachers. That course has problems that are somewhat similar. For example

1. If when working alone Smith can paint the room in 8 hours while it would take Jones 12 hours, then how long would it take them to paint the room when working together?
   
   
2. Two trains start at 7 A.M., one from Regina going to Winnipeg, the other from Winnipeg to Regina. The faster train makes the trip in 8 hours, the slower in 12 hours. At what hour of the day will the two trains pass each other? HOW IS THIS QUESTION RELATED TO #1?
   
   
3. A steamer plying between the river ports of St. Louis and Hannibal makes the trip up the river in 12 hours and the return trip in 8 hours. How long would it take a log floating past Hannibal to reach St. Louis? IS THIS QUESTION SOMEHOW RELATED TO THE PREVIOUS TWO?
   
   
4. A commuter ordinarily reaches the railroad station nearest his home at 5 p.m., where he is met by his wife in the family car. One day he unexpectedly arrived at the station at 4 p.m. and, instead of waiting for his car at the station, he started out for home on foot. After a certain length of time he met his wife and traveled the rest of the way in the car. He reached home sixteen minutes ahead of the usual time. How long did he walk? HOW IS THIS RELATED TO THE PREVIOUS QUESTION?