Hi, my name is Murray. I am a grade 10 hight school student. I'm working on a complicated proof and i need the equation for a line in 3 dimensions. I haven't got very far. Could you please give me some hints.

-thanx.

By "the" equation of a line, what is usually meant is the "parametric" equation: Given two points, say (1,6,3) and (8,2,7), you you take their difference:

This result (7,-4,4) you call the "direction vector" of the line passing through these two points. The parametric equation of the line is then

Here t is called the "parameter": imputing a value t gives you a point on the line. For instance with t=0, you get the point (1,6,3), with t=1 you get (8,2,7), with t=5/2 you get (37/2,-4,13), and so on.

You could do the same in two dimensions: With two points (1,6), (8,2), you find the direction vector (8,2) - (1,6) = (7,-4), and you get the parametric equation

To get the equation that you are familiar with, you take the two coordinate equations: the first coordinate is x = 1 + 7t, and the second is y = 6 - 4t, and you combine them to cancel out the t. For instance, 4 times the first equation plus 7 times the second equation gives you 4x + 7y = 4 + 28t + 42 - 28t = 46, so you get 4x + 7y = 46, which is the "implicit" equation of the line. It tells you, for instance, that the point (8,2) is on the line, because 4*8 + 7*2 = 46, while (9,1) is not on the line, because 4*9 + 7*1 is not 46.

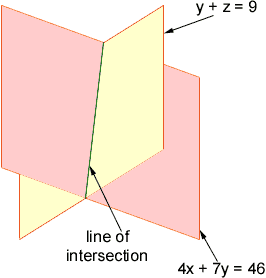
Now, to return to 3 dimensions: Lines in 3 dimensions also have implicit equations, but now it takes two equations to characterise a line. One equation alone would characterise a plane, not a line.

To find these equations, you proceed as above: the coordinate equations for

are x = 1 + 7t, y = 6 - 4t, z = 3 + 4t. As mentionned above the two first equations combine to give 4x + 7y = 46. Now adding the second equation to the third, you get y + z = 9; which is your second equation.

Together, these two equations characterise the line, it is the line of intersection of the two planes. They tell you that the point (15,-2,11) is on the line, because 4*15 + 7*(-2) = 46 and (-2) + 11 = 9, while (8,2,4) is not on the line, because 2 + 4 is not 9 (even though the first equation is satisfied).

I hope this answers your question. Good luck with your proof.