Name: Murray

Who is asking: Student
Level: Secondary

Question: Could you please explain why a vector times a vector is a scalar and how to derive the formula vector a * vector b = ab cos(a,b)

thanks alot, Murray.

Hi Murray,

There are different ways of defining a "multiplication" between vectors in the plane. If (s,t) and (u,v) are vectors in the plane you could define a multiplication, called the star product, by

(s,t)(u,v) = (su,tv) In this case (s,t)(u,v) is a vector.

You might define a multiplication, called the dot product, by

(s,t)(u,v) = su+tv Here the product is a scalar.

There is another product of vectors in 3-space, called the cross product, that gives a vector which is perpendicular to the two vectors you started with.

The second of these definitions, the dot product, turns out to be much more useful than the other two. One reason is the fact that if a and b are vectors then

ab = |a| |b| cos(a,b) where |a| is the length of a, |b| is the length of b and cos(a,b) is the cosine of the angle between a abd b.

Suppose that a = (s,t) and b = (u,v). Consider that diagram below.


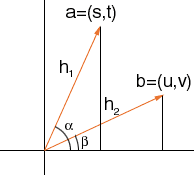
In the diagram |a| = h1 and |b| = h2 and the angle between a and b is (beta - alpha).

Pythagoras' theorem for the two triangles gives

h12 = s2 + t2
and

h22 = u2 + v2
also

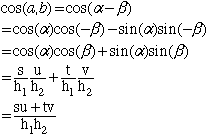
Thus

I hope this helps,
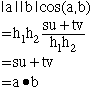
Harley
Go to Math Central