Hello,

My name is Naman and i am student .Here's my question:

There are two circles, big circle with radius R and small one with radius r. They intersect and overlap in such a way that the common area formed is 1/2 pi r ² (half the area of the small circle) If r=1, find the Radius of the big circle (R)?

If you could help me I would really appreciate it because I have contacted many people and nobody was able to help me out.

I am currently taking calculus BC and i am in 11th grade.This is just a challenge problem. Our teacher said we can solve with or without calculus. Please help me solve this problem.

Thanking you

Naman

In the diagram below the small circle has radius 1, the large circle has radius R and the two circles are tangent.

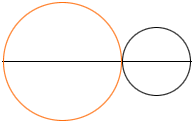
Let the small circle move slowly to the left, the large circle move slowly to the right and watch the overlap.

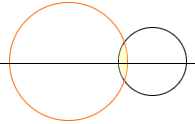
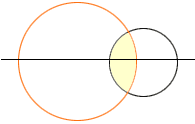
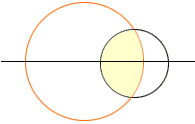
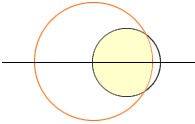
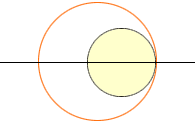
The area of the overlap region starts at zero, when there is no overlap, and continuously increases to a value of pi when the large circle completely surrounds the small circle. Somewhere along the way the area of the overlap must have been  ¹/₂ pi. Thus the answer to your question is that R can have any value larger than 1.