Hello my name is Sarah. I am a secondary student, actually a 12th grader in high school. I am having a hard time figuring out the formulas for the following problem from my claculus I class.

The problem: Water flows into a conical funnel at a continuous rate of one gallon per minute (One gallon = 231 Cu.In.). The height of the funnel is 5" and the diameter is 8".

The 1st formula: I need to develop a formula that will give the volume, in cubic inches, of the water in the funnel at any time t (in seconds). V = f(t).

The 2nd formula: I need to develop a formula that will give the height of the water in the funnel at any time t (in seconds). h = f(t).

Thank you so much for helping me.

Sarah

Hi Sarah,

The fact you need is an expression for the volume of a cone if you know its height and the radius of the top. The expression is

V = 1/3 pi r2 h where V is the volume of the cone, h is its height and r is the radius of the top. (This is one-third the volume of the cylinder with the same radius and base.)

A diagram of the funnel with some water in it is below.


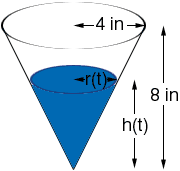
I have called the height of the water h(t) and the radius of the top of the water r(t). These are both functions of t and change as water flows into the funnel.

If you imagine a line from the center of the circle at the top of the cone to the vertex of the cone you form two triangles.


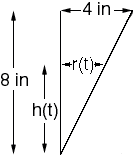
These triangles are similar so

 h(t)/8 = r(t)/4

Can you finish the problem now?
Penny
Go to Math Central