Hi. My name is Sarah. I'm a secondary student taking a Math 30C course by correspondence. The question has two parts.

The first part is:

Draw an equilateral triangle XYZ. Draw the altitude from X to YZ. Choose any point P inside the triangle or on the triangle. Draw perpendiculars from P to the sides of the triangle. The Second part is:

Measure the altitude h and the 3 perpendiculars s, t, and u to the nearest mm. Repeat as many time as is necessary until you can state a generalization concerning h, s, t, and u. If you could help me, it would be greatly appreciated.

Thank you.

Sincerely, Sarah



Hi Sarah,

The instructions are to accurately draw an equilateral triangle XYZ, construct the altitude from X, choose a point P in the triangle and construct the perpendiculars as requested. This give a diagram resembling what is below.


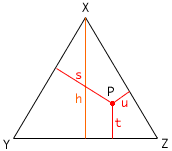
Then you are to use a ruler, measure the lengths h, s, t and u, and look for a relationship among these measurements.

The instructions seem to be saying that the relationship you arre looking for does not depend on the placemeny of P as long as it is inside or on the triangle. This makes me think to try some special choices for P first before making the measurements.

  1. What happens if P is X?

  2. What happens if P is Z?

  3. What happens if P is the midpoint of the altitude through X?

  4. What happens if P is the midpoint of XZ?

Drawing a diagram in each case shows that

  1. If P is X then s = 0, u = 0 and t = h.

  2. If P is Z then u = 0, t = 0 and s is the length of an altitude of the triangle. Since the triangle is equilateral all three altitudes are of the same length so s = h.

  3. If P is the midpoint of the altitude through X then t = h/2. What can you show about u and s?

  4. What happens if P is the midpoint of XZ?

Can you now quess the relationship among h, s, t and u? Now go back to the diagram you drew, measure h, s, t and u. Is the relationship valid in this case also?

Penny

Go to Math Central