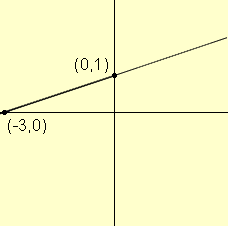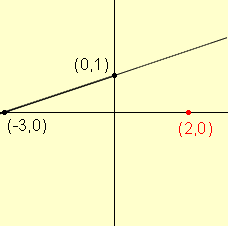| |
How do you determine that an inequality represents the area above the line and when do you include the line in the solution?
Tamara
Hi Tamara,
Suppose that the inequality is
3y < x + 3.
I would first plot the graph of the line
3y = x + 3.
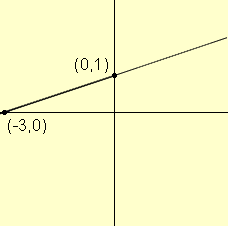
This line divides the points in the plane into 3 regions:
- the points on the line
- the points above the line, and
- the points below the line
The points on the line are the points that satisfy the equation 3y = x + 3. The other two regions are the points that satisfy 3y < x + 3 and 3y > x + 3. The question is: which is which?
To answer this question I choose some point in one of the two regions, say (2,0) which is below the line.
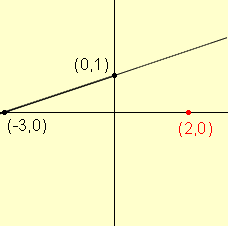
Now check to see which inequality is satisfied by (2,0). When x = 2 any y = 0 the left side is left side is 0 and the right side is 5 and 0 < 5, so
(2,0) satisfies 3y < x + 3.
Since (2,0) is below the line, the points that satisfy 3y < x + 3 are the points below the line.
If the inequality is
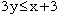 then this represents two expressions
3y < x + 3
and
3y = x + 3
The points that satisfy
then this represents two expressions
3y < x + 3
and
3y = x + 3
The points that satisfy 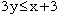 are the points that satisfy either 3y < x + 3 or 3y = x + 3. That is the points that are either below the line or on the line. Thus the line is included in the solution if the inequality is are the points that satisfy either 3y < x + 3 or 3y = x + 3. That is the points that are either below the line or on the line. Thus the line is included in the solution if the inequality is 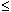 or or 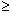 .
Penny .
Penny
Go to Math Central
|
|