Hi,
I really need help with a math problem.
The problem is:
A circle and triangle overlap as shown.the area of the circle is three times the area of the triangle.If the common region is removed,then the area of the rest of the circle would be 14 sq cm more than the area of the rest of the triangle.How many sq cm are in the area of the complete triangle.
Thanks Tara
Hi Tara,
I am going to use some letters to stand for the areas I don't know. I want C to be the area of the circle and T to be the area of the triangle. The sentence "The area of the circle is three times the area of the triangle." then says that
The next sentence talks about the area of the common region and the area of the rest of the triangle. I redrew the diagram you sent and used A for the area of the region common to the circle and the triangle, and B for the area of the rest of the triangle.
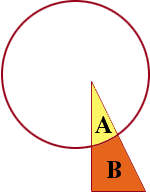
hence
The final sentence reads, "If the common region is removed, then the area of the rest of the circle would be 14 sq cm more than the area of the rest of the triangle.", that is if you subtract A from C you get 14 more than B. In other words,
Now use these three equations to find T.
The first step I would take is to add A to both sides of th last equation.
C - A + A = 14 + B + A
C = 14 + A + B
But the first equation says C = 3 x T so
and the second equation says T = A + B. Thus
Now can you find T? Penny