Name: Tava

Who is asking: Student
Level: Elementary

Question:
Hello,
I'm a grade four student from St. Mary school. In class we've been dicussing perimeters. So this is what we did; First we each got a piece of paper in the shape of the geoboards and our teacher told us to find as many different shapes of area of 12 square units. During this time we were given to find perimeters of shapes that had twelve square units one of our classmates discovered the biggest perimeter possible with twelve square units of 26 units. Another classmate discovered the smallest perimeter of fourteen units. During that time we discovered different perimeters.

What we found was fourteen all the way up to twenty-six, but they all went by two's. Why didn't they count up by 14, 15, 16, 17, 18 etc? I think it's because the area is an even number. See if you added one "block" or "square" to it you always add three because at least one of the sides is together with another side. Whyare all the perimeters all even numbers?

Thanks Bye

Thanks for your question. I will try to show you why you only get even perimeters.

When we build shapes using blocks it is easy to see that if our shape has only one block then the perimeter is 4 , an even number.

We could keep adding blocks and checking out the perimeter in each of the many shapes that we make. But rather than try to draw them all, and there would be thousands of ways if we were using lots of blocks, let's just try to think about how the perimeter changes when we add a new block.

Let's suppose that we have built a shape as in the following diagram and we have found its perimeter and indeed it turns out to be an even number.

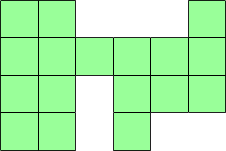
Now let's think about adding another block. We could add it in a number of different places.

• Sometimes our new block will touch our shape in just one place.
  
  
• Sometimes our new block will touch our shape in two places - when it is pushed into a corner.
  
  
• Sometimes our new block will touch our shape in three places - when it is pushed into a 'nook'.

I've labeled some examples in the next picture: when it touches in one place I've labeled that space by a 1; when it touches in two places I've labeled that space by a 2; when it touches in three place I've labeled that space by a 3. Try to think about what label I would give any of the other places that we could add our next block around the shape.

If we put our new block in a place labeled by a 1, our new block covers up one side of a block in our shape but we see that three sides of our new block are now counted in the perimeter. Thus the perimeter has gone up by 3-1 = 2. If our shape had an even perimeter before, increasing it by 2 still gives us an even perimeter.

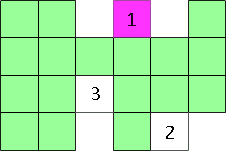
If we put our new block in a place labeled by a 2, our new block covers up two sides of blocks in our shape but we see that two sides of our new block are now counted in the perimeter. Thus the perimeter has gone up by 2-2 = 0. The perimeter hasn't changed. If our shape had an even perimeter before, it is still an even perimeter

If we put our new block in a place labeled by a 3, our new block covers up three sides of blocks in our shape but we see that one side of our new block is now counted in the perimeter. Thus the perimeter has gone down by 3-1 = 2. If our shape had an even perimeter before, decreasing it by 2 still gives us an even perimeter.

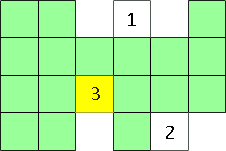
In every case, the perimeter stays even when we add our next block. Thus we will always get an even number for the perimeter of our new shape since the old shape had an even perimeter.

I hope this helps. I hope you and your classmates send us more good problems like this to Math Central.