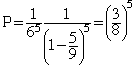Rolling 5 sevens before rolling a six or an eight

My name is Tony and I'm a senior at Memorial High. My question is; When rolling 2 dice, what is the probability of rolling 5 sevens before rolling a six or an eight?

Thanks,

Tony

Hi Tony,

The probability of rolling a seven is ⁶/₃₆

The probability of rolling a six is ⁵/₃₆

The probability of rolling an eight is ⁵/₃₆

Thus the probability of an outcome that is not a six nor an eight is 1 - ⁵/₃₆ - ⁵/₃₆ = ²⁰/₃₆

Suppose that the fifth 7 is rolled on the n^th roll and none of the previous n - 1 rolls is a five or an eight. This string of n - 1 rolls then consists of 4 sevens and n - 5 outcomes that are not fives or eights. The probability of this arrangement in n - 1 rolls is

The factor of

is necessary since you can choose 4 of the n - 1 rolls to be sevens.

n can be any positive integer larger than 4 and hence the probability of rolling 5 sevens before rolling a six or an eight is

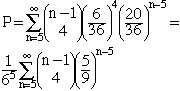
If you let x = ⁵/₉ then this expression is

You can evaluate this expression if you know Newton's form of the binomial theorem. If |x| < 1

Hence, for n = 4 this expression yields

Andrei and Penny Go to Math Central