Hi, My name is Victoria and I go to university in New Zealand, I am doing 2nd year Calculus and I am struggling, nothing my tutors demonstrate to me seems to sink in so I thought I would look for help else-where and you were recommended to me. The problem I cant figure out at the moment is: Describe the given set with a single equation or a pair of equations:

The set of points in space that lie 2 units from the point(0,0,1) and at the same time 2 units from the point (0,0,-1).

could you help?
Thanks a lot
vix



Hi Victoria,

First consider the points in space that are 2 units from (0,0,1), you can do this both geometrically and algebraically. Geometrically the set of points in space that are 2 units from (0,0,1) is the surface of the sphere with center (0,0,1) and radius 2. Likewise the set of points in space that are 2 units from (0,0,-1) is the surface of the sphere with center (0,0,-1) and radius 2. You want the points that are on both spheres. The diagram is below.


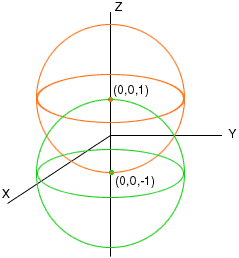
While this is a description of the given set, what is expected is an algebraic description.

Algebraically you can describe the set of points in space that are 2 units from (0,0,1) using the distance formula. If (x,y,z) is a point in space then the square of its distance from (0,0,1) is

(x-0) 2 + (y-0) 2 + (z-1) 2 Hence if (z,y,z) is 2 units from (0,0,1) then x 2 + y 2 + (z-1) 2 = 2 2 = 4 Similarly if (x,y,z) is 2 units from (0,0,-1) then x 2 + y 2 + (z+1) 2 = 2 2 = 4 You need to find the points (x,y,z) that satisfy both equations.

The form of these two equations makes them particularly nice to solve. Subtracting the second equation from the first equation gives

(z-1) 2 - (z+1) 2 = 0 You can expand the squares and solve for z or factor the expression as a difference of squares and then solve for z. In either case you find that z = 0 This means that eyery point (x,y,z) that satisfies both equations has z = 0. Geometrically the point must lie on the XY-plane.

Substituting z = 0 into x 2 + y 2 + (z-1) 2 = 2 2 = 4 gives

x 2 + y 2 + (-1) 2 = 2 2 = 4 or x 2 + y 2 = 3

This is an algebraic description of the given set. Now I can give the geometric description more explicitly. This is the circle in the XY-plane with center (0,0) and radius the square root of 3.

I hope this helps,
Penny
Go to Math Central