Subject: question in Single Variable Calculus,Stewart

I am working on question 51,section 3.7 ,page 191 of Stewart's Single Variable Calculus. The question involves a lamp post which is casting a shadow around the eliipse whose formula is x² + 4*y² = 5. I have found the derivative of the elllipse both explicitly: x/4(((5-x²)/4)^0.5) and implicitly : y' = - x/(4*y).

But I am having a mental block as far as getting the value for the height of the lamppost. I've done this question before and managed to get the right answer. But I can't remember how I did this. The implicit derivative suggests a slope of 1/4 but that's not really a solution just a guess. Can anyone help me? Please.

Werner

The key to this problem is the point I have labeled P on the diagram, the point where the line is tangent to the ellipse.

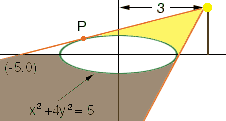
Suppose that P has first coordinate a. Find the derivative of the equation for the curve at the point P and use it to write the equation of the tangent line. This equation will contain the unknown value a. This tangent line passes through (-5,0) so if you substitute x = -5 and y = 0 into the equation of the tangent line you will have an equation for a. Solve for a.

Substitute a into the equation for the tangent line. The height of the lamp is the y-coordinate of the point on the tangent line that has x-coordinate equal to 3.