������������������������������������������������������������������������������
Adrienne
secondary (12th grade)
student
Hello,
I am having difficulty figuring out this problem. Thank you in advance, any help is much appreciated.
Water is poured into a tank in the shape of an inverted right circular cone. The height of the tank is 8 m and its radius at the top is 4 m.
a. Draw and label a picture to represent this situation. (I know how to do this)
b. Identify all variable quantities. (h = 8m, r = 4m)
c. Find an equation that relates the variable quantities, and reduce the number of variable quantities to two.
I was thinking about the equation V = 1/3 pi r2 h, which is the Volume of a cone, but I am stumped as to how I am supposed to "reduce the number of variable quantities to two." Can you point me in the right direction?
Thank you,
Adrienne
Hi Adrienne,
Here is my diagram.
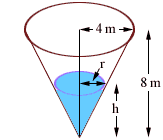
The important variables are r and h, the height and radius of the water in the cone. Then, as you said, the volume of the water in the cone is
To reduce the number of variables look back at the diagram. I see a triangle, which I have labeled ABC, with |AB| = 8 meters and |CA| = 4 meters.
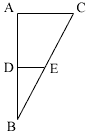
Inside is the triangle DBE with |DB| = h meters and |ED| = r meters.
The triangles ABC and DBE are similar so
If you substitute this into the equation for the volume of the water in the cone you will have an expression with the only variables being V and r.
Chers,Penny