hi

I need to calculate the standard deviation for a group of data, but I don't know in advance what is the mean. Is there a way to adjust the STDV for each datum without keeping all of the previous values? This is needed basicaly for performance, so I won't need to read twice the same data (spend processing time) nor save the previous values (spend memory).

thank you

Hi Carlos,

Two us us disagree on what you are asking so we are going to answer both of our interpretations. Hopefully one of them is the question you want answered.

First interpretation

You have some data and you have calculated the standard deviation but you don't know the mean. You now have a new observation and you want to update the standard deviation to include this new observation. Can you calculate the new standard deviation without knowledge of the mean? The answer here is no.

Second interpretation

You have some data and you want to calculate the standard deviation without calculating the mean first and then reading the data a second time. The answer here is yes as long as you can store three values while you are reading the data.

Suppose that the data set is x₁, x₂,..., x_n then the variance is given by

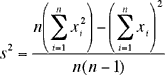
and the standard deviation is the square root of the variance. Thus, after reading the data once, you can calculate the standard deviation if you know

1. the number of observations n
2. the sum of the x_i's
3. the sum of the squares of the x_i's

Cheers,

Andrei and Penny

In March of 2004 we received the fololowing note from Britton.

While this method is correct in theory and will often work well enough, it is extremely vulnerable to the effects of roundoff error in computer floating point operations. It is possible to end up taking the square root of a negative number! The problem, together with a better solution, is described in Donald Knuth's "The Art of Computer Programming, Volume 2: Seminumerical Algorithms", section 4.2.2. The solution is to compute mean and standard deviation using a recurrence relation, like this:

M(1) = x(1), M(k) = M(k-1) + (x(k) - M(k-1)) / k
S(1) = 0, S(k) = S(k-1) + (x(k) - M(k-1)) * (x(k) - M(k))

for 2 <= k <= n, then

sigma = sqrt(S(n) / (n - 1))

Britton

Knuth attributes this method to B.P. Welford, Technometrics, 4,(1962), 419-420.

Harley

Go to Math Central