What is larger than infinity?
Dana
Hi Dana,
It depends how you define "infinity''; after all,
infinity is a trickier
concept than "three'' or "seventeen''. One definition is:
: The ideal point at the right end of the number line.
With this definition, there is nothing (meaning: no real numbers) larger than infinity.
There is another way to look at this question. It come from an idea of Georg Cantor who lived from 1845 to 1918. Cantor looked at comparing the size of two sets, that is two collections of things. Cantor said that two sets, A and B, have the same size if you can set up a perfect matching between the things in A and the things in B. If, however, any attempt to set up a matching leaves some things in B unmatched, then we say B is larger than A.
For example the sets {1, 2, 3, 4, 5, 6} and {c, l, a, u, d, e} have the same size because we can set up a perfect matching between them.
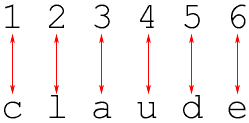
However the set {1,2,3,4,5} is larger than the set {m,a,t,h} because and
attempt to match them leaves one of the numbers 1,2,3,4 or 5 unmatched.
Cantor's idea seems really clear at first but it gives some surprising results when you apply it to infinite sets. In particular the positive integers {1,2,3,4,5,...} and the even positive integers {2,4,6,8,10,...} have the same size. Here is a perfecting matching.
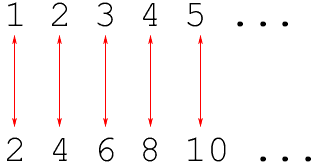
Cantor's way of comparing the size of sets is the criteria used by most mathematicians. So, how does this relate to your question? Cantor showed that no matter how large a set you have, you can always produce one that is larger. So, what's larger than infinity? Another infinity that is larger than the one you started with.
Claude and Harley