6th grade math... the problem is:

The school newspaper is interviewing 6th grade students to see what sports they follow regularly on TV. Of the 70 students interviewed; 40 enjoyed basketball; 40 enjoyed baseball; 40 enjoyed football; 20 enjoyed basketball and football; 22 enjoyed baseball and basketball; 27 enjoyed football and baseball; and 12 enjoyed all three sports. How many students out of the 70 interviewed didn't follow any one of the three sports?

My sixth grade son (and his whole family, who includes a sophomore Algebra II student) cannot come up with an answer. We need to know how to go about solving this. I know we must have to develop a graph/table of some kind... We must be putting too much information into this... or just making it too difficult. Help! My son will be asking his teacher tomorrow for help... but I need to personally know how to do this... I'm feeling really stupid right now.

Thank you, Debbie

Draw a rectangle to represent the 70 students interviewed, and inside draw three circles, one to represent each of the three sports. Make sure that you draw the circes so that they overlap to represent students who enjoy each pair of two sports and all three sports.

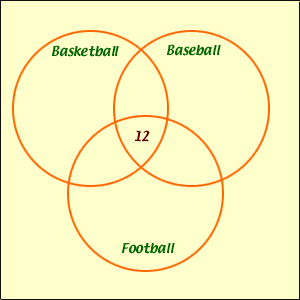
Now put the 70 students in the survey into the appropriate regions in the diagram. You know there are 40 students in the basketball circle but you don't know how to distribute them. For example how many students are in the basketball, baseball overlap but not in the overlap of all three regions? However you do know the number of students in the overlap of all three circles, "12 enjoyed all three sports". Put 12 in the overlap of all three circles.

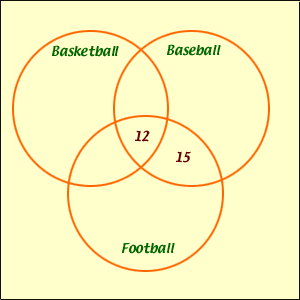
The next to the last clue reads "27 enjoyed football and baseball". This includes the 12 who enjoy all three sports so there are 27 - 12 = 15 in the region of overlap of the football and baseball circles but not in the overlap of all three circles.

Simularly 22 enjoy basketball and baseball so there are 22 - 12 = 10 who enjoy basketball and baseball but not football.

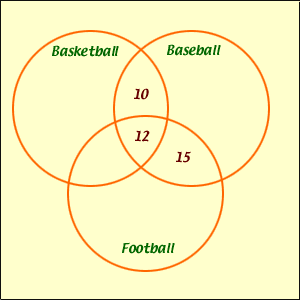
You also know that 40 enjoy baseball and from the diagram you have aready accounted for 12 + 15 + 10 = 37 so there are 3 who enjoy baseball only.

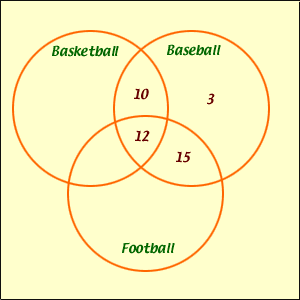
In a similar fashion fill the remaining three regions inside the basketball and football circles.

Count the number of students you have included. The students not included must be outside the circles, that is they are students who don't enjoy any of the three sports.

They must be soccer fans!

This process is part of the more general mathematical theory of 'counting' in combinatorics. It goes under the fancy name of inclusion / exclusion. If you have to do enough of these calculations, you find out when the words lead to an addition, and when they lead to a subtraction. There is a big theory, but the picture captures all the pieces - provided that you get a number which covers exactly the people inside each region of the larger image.

Go to Math Central