middle level. I am the teacher.
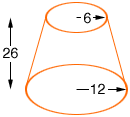
I need to make a pattern to cover an old lampshade. This is actually the bottom portion of a cone. Please help me figure out how to draw this pattern, so that we can complete our project.
Top circle diameter is 12"
Bottom/base is 24"
Height is 26"
Thank you, -Ellise :)
Hi Ellsie,
If I understand your description your lampshade looks
like the diagram below where the dimensions are in inches.
Extend the cone to its vertex, as in the diagram below, and notice the two similar triangles PQR and PST.
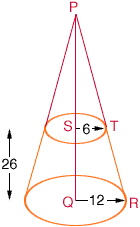
Since the triangles are similar and |QR| is twice |ST|, we must have |PQ| twice |PS|. Thus |PS| = 26 inches. Since PQR and PST are right triangles you can use the theorem of Pythagoras to find |PT| and |PR|. I got |PR| = 53.4 inches and |PT| one half of |PR|.
Slice the cone along the line RP and lie it flat to
see the pattern for the lampshade.
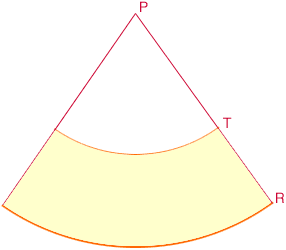
Notice that the length of the large arc through R is the circumference of the circle which forms the base of the lampshade. Thus the length of this arc is
You asked how to draw the pattern and that is exactly what I would do now. Clear a place on the floor large enough to do this and draw an arc of a circle of radius 53.4 inches. I would probably use a piece of chalk tied to the end of some string or something similar to draw the circle. Then draw a second circle, with the same centre and radius |PT|. Draw the line PR. Measure along the arc through R a distance of 75.4 inches and along the arc through T the distance you found to be the circumference of the top of the lampshade. The two points you just found, along with the point P, should lie on a line, and this completes the pattern.
I hope this helps,Penny