Which of the 4 points are collinear when you construct the following concurrent lines or rays of a triangle?
- P(1), the point where the angle bisectors intersect.
- P(2), the point where the altitudes (or extensions) intersect (inside or outside of the triangle).
- P(3), the point where the medians intersect.
- P(4), the point where the perpendicular bisectors (or extensions) of the three sides of a triangle intersect.
This is for my 9-12 high school class in geometry.
My name is Gary
Thanks for your help.
Gary
Hi Gary,
To be honest I didn't remember myself which of these four points are concurrent and I didn't have any reference material with me on the wekeend, so I used The Geometer's Sketch Pad to construct the diagram below.
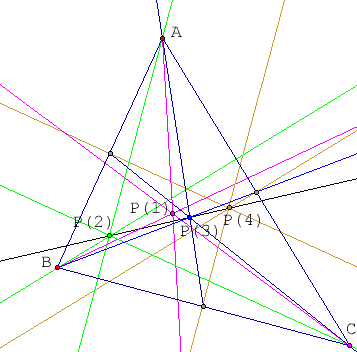
The black line joining P(3) and P(4) can be seen to pass through P(2) but not P(1). If your browser has java enabled you can open a new window that allows you to move the vertices of the triangle and observe that the line joining P(3) and P(4) always passes through P(2). [P(1) does not appear on this diagram.] A further interesting fact is that P(3) is two-thirds the way from P(2) to P(4).
Today I asked Chris and he told me it's called the Euler Line. You can find it in many geometry books, in particular H.S.M. Coxeter and S.L. Greitzer, Geometry Revisited, Random House, New York, 1967.
Harley