Quandaries and Queries
  

 

My students had a question for me today in C30 that I wasn't sure about so they suggested that I write to you. We are studying systems of equations where two conic sections are the two equations that we are solving simultaneously. We were studying the number of solutions that are possible if you have an ellipse and a parabola. We all agree that there can be none, one, two, three or four solutions. The question that the students had for me was whether or not a portion of an ellipse and a parabola can overlap and thereby allow an infinite number of solutions. What should I tell them?

Glenda

 

 

Hi Glenda,

This is a nice question. Your statement that "that there can be none, one, two, three or four solutions" lists all possible situations. Here is an algebraic argument for the situation in the diagram below. (An egg in a parabolic bowl.)

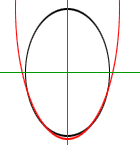
To make the equation easy, I put the ellipse in standard position, that is the centre at (0,0) and the axes along the X and Y axes. Thus the equation of the ellipse has the form

 x2/a2 +  y2/b2 = 1 and the equation of the parabola has the form y = p x 2 + q

The equation of the parabola can be written

x 2 = (y - q)/p If you substitute this expression for x 2 in the equation of the ellipse you get a quadratic in y. Since a quadratic equation has either no solutions, one solution or two solutions, the points that lie on both curves have at most two different y-values. Take the y-values you get by solving this equation and substitute them into the equation y = p x 2 + q This then is a quadratic in x and thus has either no solutions, one solution or two solutions. Thus the largest number of points you can have on the two conics is four.

More generally, any conic satisfies an equation of the form

ax 2 + bxy + cy 2 + dx + ey + f = 0. Think of x and y as values points and a, b, c, d, e and f as unknowns. You standardize it by dividing through by the first nonzero coefficient. That leaves 5 unknowns.

If you know five points on the conic then substitute in the five (x, y) pairs and you get five linear equations in five unknowns. As I recall, this system of equations will always have a unique solution. This means that if "two" conics have five points in common then they are actually the same conic. Thus two different conics can share at most four points.

Chris and Harley 		 
 

Go to Math Central