Question from student aged 11 - secondary.
Dominoes are split into two halves. If you were allowed up to 6 dots on each half, how many options of dominoes could you get?
Hi,
Suppose you have a blank domino in front of you and
you are going to put dots on it.

For the left side of the domino you have 6 choices, 1,2,3,4,5 or 6 dots. Once you have marked the left side you have again 6 choices for the right side. hence you have 6 x 6 = 36 choices for the way you mark the domino.
There is however a difficulty with this argument. Are
the two dominoes below different?
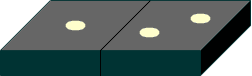

The answer of course is no, but the procedure above counted both of them. Hence the number of options for dominoes is 36/2 = 18.
Penny
In February 2007 Sam wrote to us.
The answer to your dominoes question is wrong. You state that there are 6 possibilities for each side (this is also wrong, on standard dominoes there are 7 - note "up to 6" in the question). Then the answer is given as 6 * 6 = 36, divided by two for counting both orderings. However, the "doubles" (1-1, 2-2, etc.) are not counted twice, so the answer is (6*6-6)/2 + 6 = 21. The problem becomes clear when you try to count a standard set: 7*7/2 = 24.5 pieces. The correct answers are also the triangle numbers.
--
sam
Sam is correct. I was unaware that a domino can have 0 dots so there are 7 possibilities not 6 as I stated above. Also my logic was incorrect.
Using the diagram above you have 7 choices for the left side of the domino, and then if the right side is different there are 6 choices for it. Since you can interchange the left and right side there is double counting here so you need to divide by 2. There are 7 dominos with the left side and right side identical giving a total of
(7
6)/2 + 7 = 28
a triangular number as Sam stated.
Thanks Sam,
Penny