Name: Jaylan
Who is asking: Student
Question:
Suppose you and your partner attend a party with n other couples. Several handshakes took place. No one shook hands with himself (or herself) or with their partner, and no one shook hands with the same person more than once. After all the handshaking was completed, suppose you asked each person, including your partner, how many hands they had shaken. Each person gave a different answer.
Determine how many hands did you shake and how many hands did your partner shake when n=5
Hi Jaylan,
You have n 'other' couples; then you are considering n+1 couples all told?
The problem usually is stated as having n couples, no spouses shake hands, and the 2n-1 people other than the host shakes hands with a different number of people. The question is how many handshakes did the hostess have? Let me start you on this version of the problem and you can think if your problem is the same.
If you look at a graph of this situation where people are represented by vertices and handshakes by edges the first few cases, n = 2,3,4 might lead you to conjecture (correctly) that the hostess shakes exactly n-1 hands. In the diagrams below each oval surrounds a couple, each vertex (red dot) is an individual, the edges (green lines) represent handshakes, and the blue number beside an individual indicates how many times that person shook hands.
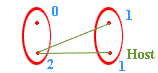
n=2
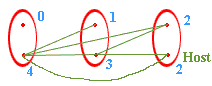
n=3
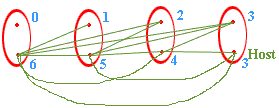
n=4
Try induction; it works but you have to be careful. Assume we've checked things out at the beginning and as an induction hypothesis have that it works for n couples, for some n ≥ 1. When looking at n+1 couples it must be that the people other than the host each shake hands exactly one of 0,1,2,3,...,2n times. (Why?) This means that there's a couple whose number of handshakes is 0 & 2n. (Why?) This can't be the host and hostess. (Why?) Remove this couple form the n+1 couples and the induction hypothesis (with all the correct assumptions on the number of handshakes) applies to the rest. The hostess is among these n pairs and by our hypothesis shakes n-1 hands but she must also shake the hand of the person who shakes 2n hands.Thus in the n+1 couple problem she shakes hands n times as required; thus the result holds for all n ≥ 1.
The (Why?)'s above aren't too obvious but try to see through them.What about the host's number of handshakes?
Good
luck.
Pennys