Quandaries
and Queries
Hi. My name is Jessica and I'm a student hoping you can answer my secondary level question. The problem given is: "For what values of the constant p does f have 3 distinct real roots?" The function is f(x)= x3 - 6x2 + p, where p is an arbitrary constant. Please help.
Thanx, Jessica
Hi Jessica,
f(x)= x3 - 6x2 has a double root
at x = 0 and a root at x = 6. If you plot the graph
when p = 0 you see that there is a minimum at some point (s,t).
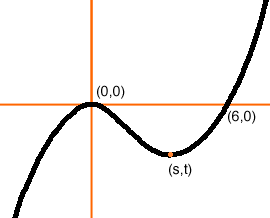
As you increase p the curve move upward giving 3 distinct real roots
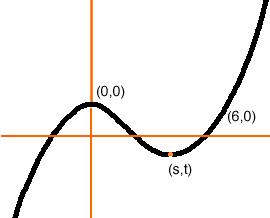
until t = 0 when you have a real root x = a < 0 and a double root at x = s.
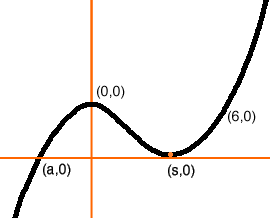
The key is to find s.
If you know some calculus you can find s by using the fact that the curve has a minimum at x = s. If not use the fact that the curve above has quation f(x) = (x - a)(x - s)2
Claude and Penny