Name: Jessica
Who is asking: Student
Level: Secondary
Question:
Solve for x. Write in interval notation.
[x2-9]/[x-5] ≥ 0
I have no idea how to do this problem.
Please help me!
Hi Jessica,
I want to consider [x2-9]/[x-5] > 0. ([x2-9]/[x-5] = 0 is easy. This can only way this can happen is if x2 = 9, that is x = ± 3.)
For [x2-9]/[x-5] > 0 to be true, either the numerator and denominator are both positive or they are both negative. This gives us two cases to examine.
Case1: x2 - 9 > 0 AND x - 5 > 0
x2 - 9 > 0 means x2 > 9, that is x > 3 or x < -3. At this point I would draw a diagram to help me "see" what is going on. The numbers x that satisfy x2 - 9 > 0 are the numbers coloured green on the number line below
![]()
x - 5 > 0 means x > 5 and thus the numbers x that satisfy x - 5 > 0 are the numbers coloured green in the number line below
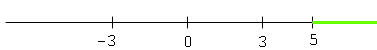
Thus the numbers that satisify x2 - 9 > 0 AND x - 5 > 0 are the numbers that are coloured green in both diagrams. These are the numbers x that satisfy x > 5.
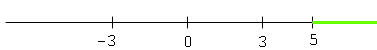
Case2: x2 - 9 < 0 AND x - 5 < 0
The numbers that satisfy x2 - 9 < 0 are
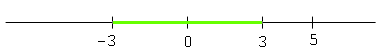
and the numbers that satisify x - 5 < 0 are
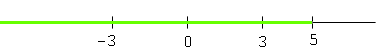
Thus the numbers that satisfy both inequalities are coloured green on both diagrams, and are hence
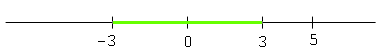
Finally the numbers that satisify the inequality [x2-9]/[x-5] > 0 fall into either case 1 OR case 2 and hence are the numbers that got coloured green by either the case 1 argument or the case 2 argument. Thus they are the numbers
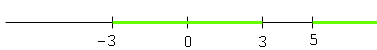
I hope this helps,
Penny