From: Josh
Why do you think it is necessary to include the "excluded values" when you write your answers to rational expressions?
Hi Josh,
When you simplify the rational expression
by cancelling the (x - 2) factors to get
you need to realize that these two expressions are not identical. When x = 2, the second expression, z = x + 2 gives a value of z = 4. The first expression however doesn't exist when x = 2 since it has zero in the denominator. What we can say is
y = z unless x = 2.
If you plot the graphs they look almost the same. The graph of z against x is
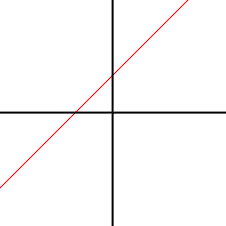
While the graph of y against x has a pinhole at (2,4). I drew a circle around the pinhole so you can see it.
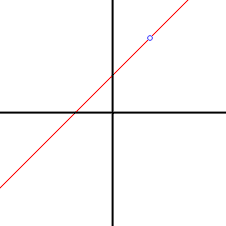
Such anomolies do sometimes arise when constructing a mathematical model of physical phenonema. Mathematical models are always approximations and some physical phenonema are modelled by expressions that behave like dividing by zero. Imagine modelling what happens when you stick a pin in a balloon, when lightening strikes a power line or when you drill well into an oil-bearing strata under the pressure of 2 kilometers of rock on top of it. In such cases it is important to know that any mathematical expression you have probably doesn't exist at the "pinhole", or at least doesn't accurately represent physical reality.
Cheers,
Penny