Quandaries and Queries
  

 

Hello there,
My name is Kathy.
my level of the question is secondary.
i am a student.

Problem:

Suppose you make napkin rings by drilling holes with different diameters through two wooden balls (which also have different diameters.) You discover that both napkin rings have the same height, h.

  1. Guess which ring has more wood in it and why.
  2. Check you guess: Use cylindrical shells to compute the volume of a napkin ring created by drilling a hole with radius r through the center of a sphere of radius R and express the answer in terms of h.

Thanks! Kathy

 

 

Hi Kathy,

This is the diagram that I see of a cross section of the napkin ring. (Actually I would describe it as a wooden bead.)


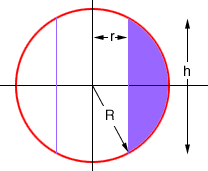
To find the volume of the napkin ring use cylindrical shells and revolve the shaded region around the Y-axis. The limits are r <= x <= R.

From the diagram you can see that Pythagoras' Theorem gives

r 2 + ( h/2) 2 = R 2 Use this expression to express the answer you get for the volume (which will be in terms of R and r) in terms of h.

Penny 		 
 

Go to Math Central