Quandaries and Queries
  

 

I have a mathematical problem I am trying to solve that involves some high level geometry/trig. I know you typically service high school levels and below. However, I am searching for guidance where ever I can.

I have a horizontal line (that is treated as a datum line or the X axis), with two circles having their center points at different heights from that line (X1,Y1 & X2,Y2). The two circles are also at different diameters (R1 & R2). Both circles and the line (X-Axis) do not intersect nor are they tangent. My goal is to determine the maximum diameter of an inscribed circle that will fit between all three.

I can easily use autocad to find this value, but I need to express it as an equation. I have researched some info on Apollonius but nothing that I can clearly apply or explains the contruction of the three tangent points to both circles and the line to construct the inscribed circle.

Attached is a sketch of the problem. The XY Origin was not define, but can be established at any place.

Thanks for any help,

Keith
Quality Eng.

 

 

Hi Keith,

I redrew your diagram and changed the notation so that one of the circles has its centre on the Y-axis. As in your description, the horizontal line is the X-axis.

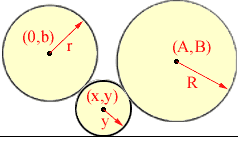
Consider the two circles in the diagram below.


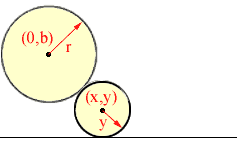
Since the distance between the centres is r + y, sqrt[x2 + (y - b)2] = r + y Thus y = (x2 + b2 - r2)/2(r + b) Hence, as the small circle moves, but remains tangent to the second circle and the X-axis, the locus of its centre is a parabola.

Applying the same argument to the pair of circle below,

we get y = [(x - A)2 + B2 - R2]/2(R + B)

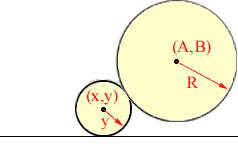
Thus the radius, y, of the circle with centre (x,y) can be found by solving

 (x2 + b2 - r2)/2(r + b) = [(x - A)2 + B2 - R2]/2(R + B) for x, and then evaluating y from y = (x2 + b2 - r2)/2(r + b)

Chris and Harley 		 
 

Go to Math Central