Hello,

Could you please help me with the following problem:
The line with equation y=mx is a tangent to the circle with equation
x²+y²-6x-6y+17=0. Find the possible values of m.
I am studying in England at A-level which is equivalent, I think, to the
last one or two years at high-school. I'm 17, anyway.

Thank you,
Lech

Hi Lech,

I completed the squares to put the equation in standard form and got

(x-3)² + (y-3)² = 1

Hence this is the circle with centre (3,3) and radius 1. The line y=mx is a line through the origin. This information allowed me to draw a diagram and see the two possible tangent lines. On the diagram P is one of the points of tangency, I called it (a,b), C is the centre of the circle (3,3) and O is the origin.

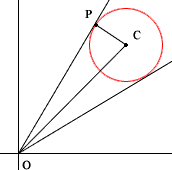
Since PO is tangent to the circle, angle CPO is a right angle and thus Pythagoras theorem ensures that

|CP|² + |PO|² = |OC|²

that is

1 + a² + b² = 18

Since P is on the circle,

a² + b² - 6a -6b + 17 = 0

Substituting from the equation above gives

6a + 6b = 34

or

b = ¹⁷/₃ - a

If you now substitute this value for b into a² + b² - 6a -6b + 17 = 0 you will have a quadratic in a which you can solve for a.

Finally find b from b = ¹⁷/₃ - a and the unknown slope is ^b/_a

Cheers,
Harley

Go to Math Central