I have been searching for
instructions on how to do this using a
compass. Can you please send instructions step by step on how to
bisect a segment into any given number of segments. (example, a way that
it will work for bisecting segment into 3, 4, or even 5 congruent parts)
Thanks,
Mandy
Hi Mandy,
The key to this construction is in the diagram below. DE is parallel to AC so the triangles ABC and DBE are similar. Thus |DB|/|AB| = |EB|/|CB|. Hence, for example, if |DB| is one third |AB| then |EB| is one third |CB|.
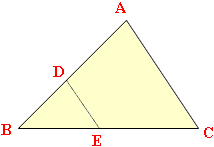
The construction for dividing the line segment BC into three congruent segments is then as follows. Draw a ray through B at any convenient angle. With the compass point on B and any convenient length draw an arc intersecting the ray through B at P. Keeping the same compass setting, move the point to P and draw an arc intersecting the ray at Q. Again, with the same setting, move the point to Q and draw an arc, intersecting the ray at A. Join A to C.
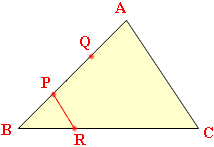
If you now construct a line through P that is parallel to AC and which intersects BC at R then |BR| is one third of |BC|. Can you construct a line through P that is parallel to AC?
Penny