My name is Marilynn
This is a high school question. I never had th opportunity to learn even simple algerbra in school. I have been trying to learn. I understand a circumfrance, diameter, and radius. I have learned what pie is and why it is called pie and that it is approximately 3.14. My son is frustrated that I can't help him with his math, The problem is this: A Circle is evenly divided into six equal triangles leaving an area between the outside of the circle and the one side of the triangle. This area is measured as 3.14. I think they used the number 3.14 to try to throw me off, knowing that pie equalls 3.14. What is the length of the radius, one line on the triangle? I wish I could draw you a picture. I hope I am clear in what I mean. It would mean so much to me if you could help me and it explaine it to me as simply as possible for my brain. Thank you so very much.
Sincerely,
Marilynn
Hi Marilynn,
First, I will tell you my assumptions about what your picture looks like:
- Each triangle has a vertex (corner) at the centre
of the circle
- Each triangle has corners on the circumference of
the circle (so, two sides of each triangle is a radius)
- The triangles share sides (there are no gapes between triangles)

The unknown area is what is left around the outside of the circle, between the circumference and the outside side of each triangle. This unknown area is split into six congruent sections (equal in every way - like the triangles are "equal" in every way - including area, length of side and length of arc). It is not clear whether you mean the area of one arc is Pi (not actually split Pie, although pronouced the same), or all six sections taken together is Pi. In what follows, I will assume that one of the outside sections has an area of Pi, so that the area of all six sections taken together is 6 times Pi. We need to find the radius of the circle, call it r.
I will also use P to stand for Pi (or approx. 3.14). Now, there is a lot of information we can garnish from the triangles:
- The angles at the center are all 60 degrees. This
is because the six angles at the center are all equal, and a circle
has 360 degrees. So do 360 edivided by 6.
- Each triangle is Isosceles. This is because two sides
are equal (the sides that are a radius).
- Each triangle, is in fact equilateral. Because it
is iscoceles, the two outside angles are also equal. But there is 180
degrees in a triangle, 60 are already used in the center angle, leaving
180-60=120 degrees for the outside angles. But, 120 divided by 2 is
60 degrees, so all three angles are equal, so it is isoscles.
- Every side in every triangle is of length r. This is because we have 6 congruent ("equal" in every way) equilateral triangles, and because two sides of every triangle is a radius.
From the geometry of the triangles, we need to do some algebra. Because we know an area, and we need a radius, we need a formula (or equation) for radius in terms of area (in what follows, keep the goal of a formula in mind). The area of the circle is P*r2 (r2 means r squared, and * means multiply) The area of the leftover sections outside the triangles, but inside the circle (an area we already no to be 6*P), can also be found by subtracting the area of the triangles from the area of the circle. We need to find an area of one of the equilateral triangles.
Method 1 for calculating an area of a triangle
The area of a triangle is b*h/2 This is where some trigonometry is needed:
Draw a line from a vertex to an opposite side that divides the opposite
side in half and is at right angles. This divides the equilateral triangle
into two congruent right angled triangles, and the new side is the height,
call it h. We need to find h.
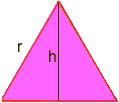
Using trig in one of the right angled triangles, we have
Method 2 for calculating an area of a triangle
Heron's formula for the area of a triangle is: sqr(s*(s-a)*(s-b)*(s-c)),
where a,b,c are the sides and s is half the perimeter Since each side
is the radius, the perimeter is 3*r, so half the perimeter is 3*r/2 Now,
the area of one equalateral triangle is: sqr((3*r/2)*(3*r/2 - r)*(3*r/2
- r)*(3*r/2 - r)) = sqr((3*r/2)*(r/2)*(r/2)*(r/2)) =sqr(3*(r4)/16)
=(r2)*sqr(3)/4 Notice that we get the same answer as method
1 - I included this in case you didn't know any trigonometry.
Recall that the area of the circle minus the area of all six triangles is the area of the leftover sections. From this we can now create an equation: P*r2 - 6*(r2)*sqr(3)/4 = 6*P Some algebra is needed to solve for r: Factor r2 on the left side (r2)*(P-6*sqr(3)/4) = 6*P Get r2 be itself by dividing: r2 = 6*P/(P-6*sqr(3)/4) Take the square root of both sides: