Quandaries and Queries
  

 

I am a draftsperson with a problem that I need some assistance with. Please help!

If given the length of an arc and the distance from the midpoint of the arc to the midpoint of a chord, how would you find the length of the chord and the radius of the arc. The chords endpoints are the same as the the arcs endpoints.
 

 

Hi,

There is no nice formula to find the radius or chord length. The best I can do is to indicate how to approximate them.

In the diagram below A and B are the endpoints of the arc, s is the length of the arc, h is the distance from the midpoint of the arc to the midpoint of a chord and theta is the angle subtended by the arc at the centre if the circle.

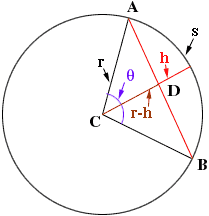
If theta is measured in radians then

s = r theta and hence the measure of angle ACD is theta/2 = s/2r. Thus cos( s/ 2r) = (r - h)/r

You can now substitute the values you have for s and h into the expression above and use an approximation procedure to solve for r. Once you have r you can use the theorem of Pythagoras on the triangle ACD to find the length of DA which is half the chord length.

I hope this helps,
Penny
 
 

Go to Math Central