The measure of each interior angle of a regular polygon is eight times that of an exterior angle of the polygon. How many sides does the polygon have?
I found this using the formula to find the interior angle (n-2)180/n
and the formula for the exterior angle which is 360/n. n is the number
of sides.
I have already determined that the answer is 18 sides, but is there
a simpler formula you could use to solve this problem?
Thanks for your help!
Melissa
Hi Melissa,
I'm not very good at remembering formulas. I would do this with a diagram.
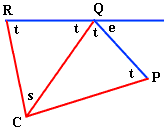
PQ and QR are two adjacent sides of the polygon, C is the center of the polygon and e is an external angle. If there are n sides to the polygon then the angle RCQ (the angle s) is 360/n degrees. The angles labeled t are all equal and you know that 2t = 8e.
2t + e = 180 degrees and 2t + s = 180 degrees and hence s = e.Hence
180 = 2t + e = 8e + e = 9e = 9s = 9
360/n
and thus n = 18.
Cheers,
Penny