This is Nadene (student), and I'm having difficulty trying to solve a pre-cal question (high school).
The question is:
Prove the identity. cos [x + (y-pi/2)] = sin (x+y)
A hint was also provided which is: "Apply cos (alpha + beta) first then within that apply cos (alpha-beta)"
Any help on solving this will be greatly appreciated.
Thank you
Hi Nadene,
I can see three ways to prove this identity and the way suggested by the hint is, in my opinion, the worst of the three. The proof, suggested by the hint, goes as follows:
cos(s+t) = cos(s)cos(t) - sin(s)sin(t)
and sin(s+t)=sin(s)cos(t)+cos(s)sin(t)Let s = x and t = y - pi/2 and apply the first of the expressions above to get
cos [x + (y-pi/2)]=cos(x)cos(y-pi/2)-sin(x)sin(y-pi/2)
Now let s=y and t=pi/2 and apply the expressions above for cos(s+t) and sin(s+t). Simplify using the values of cos(-pi/2) and sin(-pi/2) and you will get an expression that is equivalent to sin(x+y).
The second proof is simpler.
Write cos [x + (y-pi/2)] as cos [(x + y)-pi/2)] and use the expression for cos(s+t) with s=x+y and t=-pi/2. Simplify using the values of cos(-pi/2) and sin(-pi/2).
The third proof is, in my opinion, the easiest.
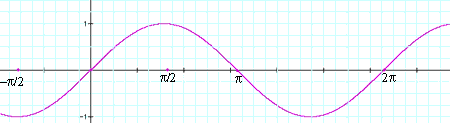
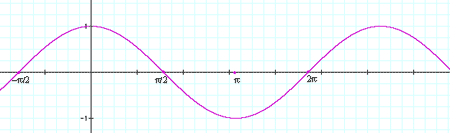
Plot the graphs of y=sin(t) and y=cos(t).
y=sin(t)
y=cos(t)
To get the graph of y=cos(t-pi/2) you shift the y-axis pi/2 units to the left to get
y=cos(t-pi/2)
But this is the graph of y=sin(t) and hence for any t, cos(t-pi/2)=sin(t).
Cheers,
Penny