Subject: Sums of Evens

How do I find a geometric way to easily compute sums of consecutive even numbers 2 + 4 + 6 + ....



Hi Rosa,

The first part of our answer to your question comes from the notes for an online class here at the University of Regina. The problem was to find the sum 1 + 2 + 3 + ... + 5000. The solution begins:

Understand the Problem: This problem is stated quite simply as an arithmetic problem and we are to find the total of all the whole numbers from 1 to 5000. One way of doing this problem is simply to add the numbers one at a time, which would take 4999 steps. Obviously, we are not expected to do this much work (and our human nature should tell us to avoid this much work), so we have to look for a shortcut.

Devise a Plan: This problem, or at least the shortcut, is best solved by inventing a new and creative approach.

Start with a smaller problem

Carry out the Plan:

First, we'll show how to sum 1 + 2 + 3 + 4 + 5 as follows. If we count the blocks in the array, we will see that the sum is 15.

Be creative

The creative, new approach is a famous technique attributed to Carl Friedrich Gauss (1777 - 1855). Gauss amazed his teachers in elementary school by seeing quickly how to sum the integers from 1 to 100.

If we have two copies of the block array above we can flip one over and stack them to create a rectangle.

This rectangle is 5 blocks wide and 6 blocks high.

The number of blocks in the rectangular array is

   (1 + 2 + 3 + 4 + 5)
+ (5 + 4 + 3 + 2 + 1)

Which is equivalent to

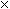2(1 + 2 + 3 + 4 + 5) = 5 6 = 30
1 + 2 + 3 + 4 + 5 = 30/2 = 15

The rectangular array is five columns of 6 blocks each. The same structure can be seen in the numeric array

   (1 + 2 + 3 + 4 + 5)
+ (5 + 4 + 3 + 2 + 1)

where there are 5 columns of numbers and the sum of each column is 6.

The notes then go on to find 1 + 2 + 3 + ... + 5000.

The first n natural numbers can be derived using this numeric array:

Write out the sum forwards:

1+ 2+ 3+ ....+ (n - 2)+ (n - 1)+ n
Now write it out backwards:
1+ 2+ 3+ ....+ (n - 2)+ (n - 1)+ n
n+ (n - 1)+ (n - 2)+ ....+ 3+ 2+ 1
Now add up the columns as they line up:
1+ 2+ 3+ ....+ (n - 2)+ (n - 1)+ n
n+ (n - 1)+ (n - 2)+ ....+ 3+ 2+ 1
__________________________________________________
(n + 1)+ (n + 1)+ (n + 1)+ ....+ (n + 1)+ (n + 1)+ (n + 1)

Note: there are n terms being summed, each of which is (n+1) so the sum of the forwards and backwards together is n(n+1). But that is twice the sum of 1 to n since we added it up forwards and backwards so to get the sm of 1 to n, we need to divide by two. Hence the formula is  n(n+1)/2.

A similar approach can be used to find the sum of the first n even numbers. Use a geometric array of blocks as in the diagrams above or a numeric array obtained by writing the sum forward and backwards and then adding the columns.

Leeanne and Harley

Go to Math Central

To return to the previous page use your browser's back button.