I have this question and i dont know how to do it. i noticed there is a question on your site similar to this but that question did not deal with polar co-ordinates. I would be able to draw it but is there a way to do it mathimatically. Or is the best way to do it, to find the grdient of the line, then find the inverse gradient because that is the gradient of a perpendicular line. Then with that gradient i could find the equation of the line then possibly find out the point. Im not sure this is the right way as im thinking there must be a way to do it with complex numbers.
The question is as follows: The vertices O and A of an EQUILATERAL triangle OAB in the complex plane are located at the origin and 3 + 3i. Find all possible values for the complex number representing the vertex B. Give the location of B in both polar and cartesian form (to 2.d.p)
I drew the points on a graph and found that there are only two points that B can be and they are eual distances from O and A. the distance is the same as OA, which is (root)18.
I only managed to draw the points on the graph but i dont kno how to do it mathmatically.
Hi Scott,
The method that you describe using the gradient of the line from O to A will work, but I think that working in polar coordinates is easier. I drew one of the possible locations for B in the diagram below.
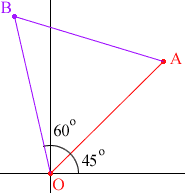
As you already know the distance from O to A is sqrt(18) so the distance from O to B is also sqrt(18). From the diagram you can see that the angle which OB makes with the real axis is 105o, and hence, in polar notation, B is the point (sqrt(18), 105o). Hence, in the complex plane, B is sqrt(18)
You can try the second location for B.
Cheers,Penny
Here is an answer from Chris that is even more direct,
Chris