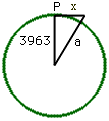There are 2 six foot men. What would the distance be between them before one could not be seen because of the curvature of the earth?
My grandson, who is stationed in Baghdad, Iraq, asked the question. This is one of the fun problems his unit was discussing. Thanks for your time.
Submitted by Shirley

In April 2004 we received an message from Jerry, a retired Engineer, who pointed out an error in my solution above. What follows is a slightly edited version of what Jerry sent.
It is true that Harley showed quite correctly that the earth curves approximately 8 inches in one mile. The solution presented then goes on to find out over how many miles does the earth curve 72 inches or 6 feet. Then this distance is doubled which is required (and would be easy to forget), because each man looks this distance to his horizon, where the line of sight is tangent to the earth's surface midway between them. All of this reasoning is correct so far.
However, it turns out that while the earth does curve 8 inches in one mile, it does not take 9 miles to curve 72 inches. To show this, let us return to the Pythagorean Theorem method used by Harley, but using 6 feet for the curvature. Here is a copy of Harley's diagram with the 1 in the diagram replaced by x, since in this case the distance is unknown.
Again, using the theorem of Pythagoras
a2 = 39632 + x2 = 15705369 + x2
Solving for x,
x2 = a2 - 15705369
a must be 3963 miles + 6 feet (Let's say the men are actually 6'3", so their eyes are six feet above ground.). Thus
a = 3963.001136 milesx2 = 15705378 - 15705369 = 9
x = 3 milesNow, remember that each man looks 3 miles to the horizon, giving their distance from each other as 6 miles.
This shows that at eye level of 6 ft. the horizon is 3 miles (at sea or on a level plain).
A rule-of-thumb for line of sight problems such as this, where the distance is small in comparison to the size of the earth is
c = (2/3) times x2, where x is distance in miles and c is curvature in feet.
For the problem at hand, we then have x2 = (3/2)c
x2 = (3/2)
6 = 9
x = 3This is the same result that the more lengthy solution yielded.
--Jerry
Thanks Jerry,
Penny
To return to the previous page use your browser's back button.