Name: Stan

Who is asking: Student
Level: All

Question:
What two different base lengths can an isosceles triangle have with sides on both remaining at 13 inches? How do I show this?



Hi Stan,

This is a problematic question, since there are an infinite number of possible base lengths, not just two different base lengths. To find one possible base length, pick an angle between 0 and 180 degrees to serve as the angle between the two sides of length 13 inches of the isosceles triangle. I will pick 60 degrees. Now use the cosine law. If b represents the length of the base in inches, then:

b 2=13 2 + 13 2 - 2(13)(13)cos60

b = 13 inches Note that this answer makes sense: all angles work out to be 60 degress, so it is a equilateral triangle.

I we chooses the angle between the equal sides to be 30 degress (instead of 60), using the cosine law, the base is approximately 6.7 inches. If the angle is 120 degrees, the base is approximately 22.5 inches. ETC.

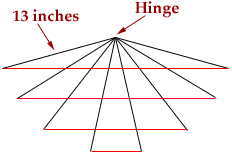
If you imagine two 13 inch long sticks hinged together at one end then you can form infinitely many different triangles by just changing the angle at the hinge.

Paul and Penny

Go to Math Central

To return to the previous page use your browser's back button.