Hi Guys,

I have to work out the dimensions and arcs of a cone that is cut off at the top.

I.e Top diameter is 33mm to bottom diameter is 43mm and the depth is 80mm

Are you able to work what the flat of this cone would be as I need to design within the flat area and then have it cut out.

I really need to know what the flat of it is before it is cut and curled to form the above cone.

Does this make sense.

I'm not at school and would appreciate the assistance with this mathematic query

Thanks.

Kind regards,
Stuart

They key step is to consider the cone cut open and laid out flat in the plane.

If you took the original cone - then this would be a sector of a circle. You need to work out the radius of that circle and the angle of the sector.

The cut off cone is just a variant - you cut out a smaller radius circular sector (same angle, smaller radius) and are left with a piece of an annulus - the region between the large circle and the small.

The easiest measurements to work with would be what in 3-D is the 'slant height' - the length from the vertex of the cone to the outside bottom of the cone. This is the radius for the circle.

If all you have is the diameter of the base circles of the cone, and the 'depth' (is that the height of the cut off piece - the frustrum)? then you need to work out some plane geometry with pythagoras theorem.

I can only offer one sample, because I am not sure what 'depth' means. I will take this as the description of an isosceles trapezod formed by cutting with a plane down the middle of your object. The 'height' of this piece is then 80 mm. The base is the larger diameter (43 mm) and the top is (33 mm).

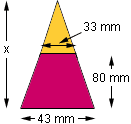
You really need to place this into a larger triangle from which you can work out the slant heights, and the angles in the flat piece. If you extend the sloped sides of this trapezoid, they will meet at a point along the center line of the figure. You can see what the height of the larger triangle is by proportions (trig is possible but not necessary here). As you moved up 80 mm, you reduced the width by 10 mm. If you want to reduce it to 0 (make a triangle) you need to solve  ^x/₄₃ = ⁸⁰/₁₀. That makes x = 8  43 = 344 mm. Cut this triangle in half to make a right angled triangle, you have base  ⁴³/₂, and height 344. With pythagoris, you can find the length of the hypotenuse X= (square root of 22.5 ² + 344 ²).

This is the radius of the plane circle you will work with. The angle of the plane sector is found by the ratio of the circumference of your actual base of the cone (pi  43) to the circumference of the plane circle (pi  X) multiplied by whatever units you want for angles (e.g. 360 for degrees).

Finally, you need to repeat the calculation of X, but with the smaller base (the top cut off the cone) of  ³³/₂, to get Y - the radius of the smaller circular segment cut off from your cone.

Does that help?

Walter Whiteley
York University