Tom
Student
I have two circles, different sizes a known distance from each other. We know the radii of the circles. How do I construct a line that is tangent to both circles relative to the segment that connects the centers of both circles?
Thanks
Hi Tom,
First you need to know how to construct a tangent to circle, through a point outside the circle. In the diagram below the circle with centre C and the point P are given. Let Q be the midpoint of the line segment joining C and P and draw the circle with centre Q and passing through P and C.
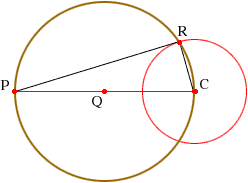
Let R be one of the points where the two circles intersect and construct the triangle RPC. The angle at R is a right angle and hence PR is tangent to the original circle.
Now return to your problem. The diagram below shows the two circles with centres C and D. Draw a diagonal AB through the smaller circle and a diagonal ST through the lrager circle, parallel to AB. Join SA and extend this line to meet DC extended at the point P. Notice that triangles APC and SPD are similar.
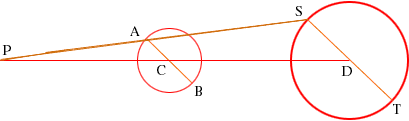
Use the construction above to construct a tangent to the circle with centre C and passing through P. Show that this line is also tangent to the circle with centre D. Chris and Penny
To return to the previous page use your browser's back button.