Name: Veronica

Who is asking: Student
Level: Secondary

Question:
Solve the following inequality:

5(xsqured-4)/(xto the 5th(2x-5)to the 3rd) < or equal 0

Solve the following equations for all roots

square root of x+2=-1+square root of 2x+3

what's ZERO FACTOR PROPERTY???

The hypotenuse of an isosceles right triangle is 7cm. long. Determine the lenghts of the other sides.



Hi Veronica,

Since we are dealing with a rational expression, the expression as a whole will be < 0 when the numerator is positive and the denominator is negative, or when the numerator is negative and the denominator is positive. We will begin by determining the intervals where the numerator is positive and where it is negative. Then we will determine the intervals where the denominator is negative and where it is positive. Then we will see where the intervals overlap (if they overlap at all) such that the numerator is positive for the same values as where the denominator is negative, and vice versa.

5(x 2 - 4) = 0 when x 2 - 4 = 0 because we can divide 5 from both sides. So we have:

x 2 - 4 = 0
x 2 = 4           Add 4 to both sides
x = +2, -2      Take the square root of both sides

Now set up a number line and test values in the following intervals (-infinity, -2), (-2, 2), and (2, + infinity) to see if 5(x 2 - 4) is positive or negative in those intervals:

(-infinity, -2): choose -3

5[(-3) 2 - 4] = 5(9 - 4) = 5(5) = 25 a positive value, so 5(x 2 - 4) is positive for all values from -infinity up to -2

(-2, 2): choose 0

5(0 2 - 4) = 5(0 - 4) = 5(-4) = -20 a negative value, so 5(x 2 - 4) is negative for all values from -2 to +2

(2, +infinity): choose 3

5(3 2 - 4) = 5(9 - 4) = 5(5) = 25 a positive value, so 5(x 2 - 4) is positive for all values from +2 to +infinity

Divide your numer line into the three intervals and put a "+" sign above those intervals where we found the numerator to be positive and a " - " above the interval where we found the numerator to be negative.

Now we do a similar process with the expression in the deonominator. The Zero Product property states that if two factors a and b when multiplied together give a product of zero, then either a = 0, b = 0 or both a and b equal 0. In symbols, if ab = 0, then a = 0 or b = 0 or a = b = 0. We will use this property to help us with the expression in the denominator.

If x 5(2x - 5) 3 = 0 then x 5 = 0, or (2x - 5) 3 = 0 or both of them equal 0.

If x 5 = 0, then x = 0 by taking the 5th root of both sides.

If (2x - 5) 3 = 0, then (2x - 5) = 0 by taking the cube root of both sides

2x = 5 by adding 5 to both sides
x =  5/ 2 by dividing both sides by 2.

Draw a second number line below your first number line. Now we can set up and test values from our intervals (-infinity, 0), (0, 5/2), and (5/2, +infinity):

(-infinity, 0): choose -1

(-1) 5[2(-1) - 5] = -1(-2 - 5) = -1(-7) = 7 a positive value so the denominator is positive for all values from -infinity to 0 (this is the same as saying "all negative values")

(0,  5/ 2): choose 1

1 5[2(1) - 5] = 1(2 - 5) = 1(-3) = -3 a negative value so the denominator is negative for all values from 0 to 5/2

(  5/ 2, +infinity): choose 3

3 5[2(3) - 5] = 243(6 - 5) = 243(1) = 243 a postive value so the denominator is positive for all values from  5/ 2 to +infinity (this is the same as saying "all values greater than  5/ 2")

Divide your second numer line into the three intervals and put a "+" sign above those intervals where we found the denominator to be positive and a " - " above the interval where we found the denominator to be negative.

Now compare the two number lines to see where a positive interval on the first number line overlaps with a negative interval on the second number line. You should find 1 such overlapping interval: (2, 5/2).

Now compare the two number lines to see where a negative interval on the first number line overlaps with a positive interval on the second number line. Again you should find 1 such overlapping interval: (-2, 0).

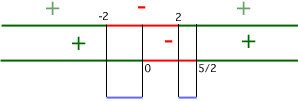
Therefore, the entire expression as a whole is less than zero when x lies on either interval (2, 5/2) or (-2, 0).

To solve your second problem, square both sides to eliminate the radical from the left hand side. The right hand side must be squared using FOIL or the distributive property and will still contain a radical. Group all non-radical terms on one side of the equation and square both sides again to eliminate the final radical. The non-radical terms will likely be squared using FOIL again. The expression you are left with will need to be set to zero and factored. Then use the Zero Product property to find the roots from the factors you get. Be sure to test all roots found by substituting them back into the original expression. Some may not work since the squaring may have created extraneous roots.

For the third problem, consider what an isosceles triangle looks like: 2 sides are the same length. Since it is a right triangle, the hypotenuse is the longest side, and each leg is the same length. Using the Pythagorean Theorem, hypotenuse squared = leg squared + leg squared, draw a diagram. Label the hypotenuse "H" and the legs each as "L" since they are the same length. The equation you need to solve is H 2 = L 2 + L 2 = 2L 2 when H = 7 so solve: 49 = 2L 2.

Hope this helps,

Leeanne



Go to Math Central

To return to the previous page use your browser's back button.