According to page 126 of Murtha & Willard's "Statistics and Calculus" (Prentice-Hall, 1973), Newton's binomial theorem can proved inductively. I suppose that was his method, which I would like to see.
I am not knowledgeable enough to supply a rigorous proof, but the coefficients of the expansions do follow a satisfying pattern when (1+x)n+1 is compared to (1+x)n. If calculus is required, I would like to know why.
Hi,
You certainly don't need calculus, just some facility in working with factorials. The theorem says that, if n is a positive integer and k is an integer with 0 ≤ k ≤ n, then the coefficient of xk in the expansion of (1+x)n is C(n,k) = n!/k! (n-k)!. . (To make this true in all cases you have to agree to write 1 for 0! and for x0.)
The induction is on n. Start the induction with n = 1. (1+x)1= 1+x and the possible values of k are 0 and 1. You can check that C(1,0) and C(1,1) are both 1.
For the inductive step assume that for a fixed value of n, the coefficient of xk in the expansion of (1+x)n is C(n,k) = n!/k! (n-k)!. The task now is to show that in the expansion of (1+x)n+1 the coefficient of xk is C(n+1,k).
(1+x)n+1 = (1+x)(1+x)n and hence the term with x to the power k comes from two sources,
- 1 times the xk term in the expansion of (1+x)n
- x times the xk-1 term in the expansion of (1+x)n
According to the inductive assumption the coefficients are
- 1
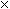C(n,k) - 1 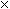C(n,k-1)
Thus the coefficient of xk in the expansion of (1+x)n+1 is
C(n,k) + C(n,k-1)
= n!/k! (n-k)! + n!/(k-1)! (n-(k-1))!
= n!/k! (n-k)! + n!/(k-1)! (n-k+1)!
= n!(n-k+1)/k! (n-k)!(n-k+1) + n! k/k (k-1)! (n-k+1)!
= n!(n-k+1)/k! (n-k+1)! + n! k/k ! (n-k+1)!
= C(n+1,k)
Cheers,
Penny