The base of a pyramid-shaped tank is a square with sides of length 9 feet, and the vertex of the pyramid is 12 feet above the base. The tank is filled to a depth of 4 feet, and water is flowing into the tank at a rate of 3 cubic feet per second. Find the rate of change of the depth of water in the tank. (Hint: the volume of a pyramid is V = 1/3 B h , where B is the base area and h is the height of the pyramid.)
Please HELP!

Thanks in advance.
Annette/Teacher
(first year teaching calculus)

Hi Annette,

I drew a diagram of your tank with the assumption that pyramid-shaped means that the vertex of the pyramid is above the center of the square base.I labeled three of the points, the vertex V, the point on the base directly below the vertex P and the midpoint of one of the sides of the base Q.

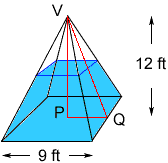
The right triangle VPQ has height |VP| = 12 ft, and base |PQ| = ⁹/₂ ft.If h(t) is the height of the water at time t seconds then I can sketch the triangle and label it.

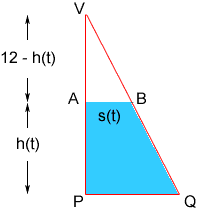
In the diagram AB is the waterline. Triangles VPQ and VAB are similar and hence

 ^|VP|/_|PQ| = ^12-h(t)/_s(t)

and hence

s(t) = ³/₈ (12 - h(t))

The top surface of the water has area (2 s(t))² = 4 s(t)² and hence the volume of water in the tank is

V(t) = ¹/₃ 81 12 - ¹/₃ 4 s(t)²  (12 - h(t))

= 324 - ³/₁₆  (12 - h(t))³

Hence

V'(t) = - ⁹/₁₆  (12 - h(t))² h'(t)

V'(t) = 3 cubic feet per second and h(t) = 4 feet when you want to find h'(t), thus you can solve for h'(t).

I hope this helps,
Harley

Go to Math Central