Who is asking: Student
Level: Middle
Question:
The area of the top of a closed rectangular box is 252cm2, the area
of the front of the box is 105cm2, and the surface of the box is
834in2 (or 5380.64cm2). What is the volume of the box?
Hi,
The surface of box comes in six pieces, the top and bottom, the front and back and the two ends. In your box the top and bottom each have area 252cm2 and the front and back each have area 105cm2. The surface area of the entire box is 5380.64cm2 and hence the area of the two ends together is
5380.64 - 2
252 - 2
105 = 4666.64 cm2
and hence the area of one end is
4666.64/2 = 2333.32 cm2
I need variable names to go any further so I drew a diagram and labeled the lengths of the edges.
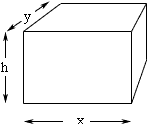
Using my notation and the information above we have
xy = 252
hx = 105
hy = 2333.32
You want to evaluate hxy to obtain the volume of the box.
Here is one way to proceed.
Use the first equation to write y in terms of x:
y = 252/x
Use the second equation to write h in terms of x:
h = 105/x
Substitute these values of y and h into the third equation and solve for x.
Once you find x, y and h and calculate the volume check you answer by going back and verifying that the surface area is 5380.64cm2.
Penny