Name: benjamin
Who is asking: Student
Level: Secondary
Question:
How do I find the points of intersection of the two functions:
1) y = 2 - (e^-x)
2) y = 1 + (x^2)
I know that I have to set them equal to each other, but I can't solve
for x. Please help :-)
Hi Benjamin,
Setting them equal gives
2 - e-x = 1 + x2
1 - x2 = ex
At this point, like you, I see no technique to solve for x. All I can do is use my number sense and try some values of x. This yields an immediate result since the fact that e0 = 1 shows that x = 0 is a solution.
A harder question is "Is there another solution?" To do this I used some computer software to plot the two functions
f(x) = 2 - e-x , and
g(x) = 1 + x2
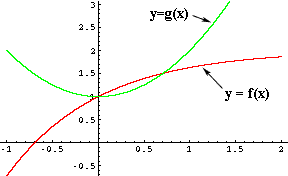
From the plot I can see that x = 0 is a solution, but also that there is another solution at approximately x = 0.7. My calculator gives f(0.7) = 1.50341 and g(0.7) = 1.49, so they are not equal, but close. The best I can do now is improve my approximation. Try x = 0.71 and see what you get.
Penny