We've been having problems on related rates and this one has so little going on in it, that I have no clue what to do. I don't see any relationships such as volume or area that I could use to figure it out.
A baseball diamond is the shape of a
square with sides 90 feet
long. A player running from second to third base at a speed of 28
feet/ second is 30 feet from second base. At what rate is the
player's distance from home plate changing?
Please help! Thank you so much.
Bethany
12th grade student
Hi Bethany
A baseball diamond is in the shape of a square. I think the natural way to draw it is with home plate at the origin and the first base line at a 45o angle to the x-axis. That means the the base lines are lines with slopes +1 or -1. It is easier to write the equations of lines that are horizontal or vertical so I drew my diagram with home plate at the origin, and the first base line along the x-axis.
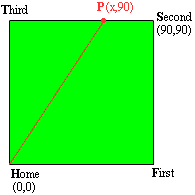
P is the position of the runner and has coordinates (x,90) where x is a function of time, t. x is measured in feet and t in seconds. You want the rate at which the distance from Home to P is changing. This distance I will call |HP|.
Use the distance formula to write the distance |HP|, and then differentiate this expression with respect to t. This will give you d|HP|/dt . Evaluate this expression when P is 30 feet from Second. Notice that x is the distance from P to Third and hence x is decreasing so dx/dt = -28 feet/sec.
Penny