I am a teacher for grades 10-12. 

Name:  Bruce
 
A polynomial is defined as
Polynomial functions are functions that have this form:
f(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀
The value of n must be an nonnegative integer. That is, it must be whole number; it is equal to zero or a positive integer.
The coefficients, as they are called, are a_n, a_n-1, ..., a₁, a₀. These are real numbers.

Questions: 

1. why must n be positive?
   
2. what are some historical facts about the evolution of the definition?

Hi Bruce,

There are some web pages maintained by Jeff Miller, a teacher at Gulf High School in New Port Richey, Florida, that are a wonderful resource for historical questions and questions about mathematical termonology. Go to his page, Earliest Known Uses of Some of the Words of Mathematics and search under P for polynomial.

Polynomials, defined as you have done above, have many nice properties. One of these is that the domain of a polynomial is the entire real line. That is if f(x) is a polynomial and s is a real number then f(s) is a real number. On the other hand if f(x) has a term with a negative power of x then f(0) is not a real number.For example if f(x) = x^-1 then f(0) is undefined and the graph of f(x) is in two pieces.

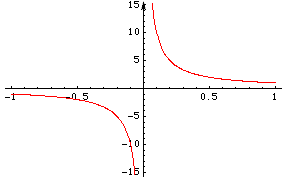
f(x) = x^-1

Polynomials play a role in the development of functions, somewhat analogous to the role that the integers play on the real line.If you add, subtract or multiply two polynomials you get another polynomial. We know that, with the integers, if we want to allow division of any two integers then we must expand our numbers to include the rationals. Even here there is a problem since division by zero does not result in a number. Likewise with polynomials, if we want to allow division of any two polynomials then we must expand the class of functions and, as in the example above of the polynomial 1 divided by the polynomial x, the resulting function may produce outputs that are not numbers.

Functions that can be written f(x) = ^p(x)/_q(x) where p(x) and q(x) are polynomials are called rational functions.

The functions of the form f(x) = a_nxⁿ + a_n-1x^n-1 + ... + a₁x + a₀
where the value of n must be an nonnegative integer, have nice properties and are natural building blocks for the construction of other functions, and as such deserve their own name.We call them polynomials.

Harley

Go to Math Central