Quandaries
and Queries
My problem is as follows:
An isosceles trapezoid with bases of lengths 12 and 16 is inscribed in a circle with a radius of 10. The center of the circle lies in the interior of the trapezoid. Find the area of the trapezoid.
Thanks for your help!
Bruce
I am a student-teacher
Grade level 9th to 12th
Hi Bruce,
The area of a traposoid is the average of the lengths of the parallel sides times the distance between the parallel lines. I drew a rough sketch of your situation.
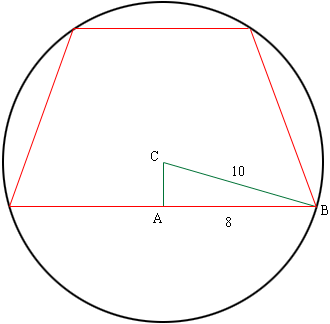
C is the center of the circle and triangle ABC is a right triangle so you can use Pythagoras' theorem to find |AC|. Can you complete the problem now?
Penny